화성학 레슨 - Lesson 5. 음정 (Interval) II - 전회음정, 겹음정

“선생님 혹시 드럼패드 사용하세요?”

“드럼패드는 갑자기 왜?”

“친구가 MPC를 샀는데 좋아보이더라구요.”

“MPC는 흑인음악 하기에 좋지. 드럼패드 역할도 되고 샘플러 기능도 있고 시퀀싱 기능도 있어서 잘 쓰면 좋은 악기야.”

“그렇군요. 음원이 없는 MPD가 가격이 괜찮길래 그걸 사볼까 했어요. 미디 선생님이 권해주시더라구요.”

“그런데 나는 그런거 안써.”

“안좋은가요?”

“안좋은게 아니고 잘 못써서 그래. MPC의 진짜 장점은 댐핑감과 그루브감에 있는데 MPC를 잘 못다루니 별 차이가 없더라구. 드럼도 실시간 연주안하고 거의 마우스로 찍는 편이고 시퀀싱도 큐베이스로 다 해버리니까 뭐 별로 필요가 없더라고.”

“말씀을 듣고나니 고민되네요.”

“뭐 그래서 MPC사는 사람도 많지만 파는 사람도 정말 많지. 악기를 살 때는 그 악기의 장단점이 뭔지 잘 파악하고 사야돼. 나도 한 때 악기모으는데에 시간 많이 쏟았는데 악기 하나를 계속 파는게 훨씬 도움이 되더라. 내가 내고 싶은 소리가 있는데 내가 가진 악기로는 그 소리를 낼 수 없을 때, 그 때 악기를 사야지. 악기부터 사놓고 자기 음악이 좋아질거라고 기대하는 건 신부도 없이 예식장부터 잡아놓는 꼴이라고 주모 작곡가가 얘기하더라. 물론 어느정도 범용 악기는 가지고 있으면 좋겠지. 뭐 곡은 안쓰고 악기만 사모으는 사람들한테 하는 얘기였을거야.”

“주모 작곡가면 주영훈인가요?”

“주씨가 주영훈 밖에 없나? 어쨌든 나도 동의하는 의견이야.”

“그렇군요. 그런데 주영훈씨도 잘하나요? 이미지 봐서는 별로일 것 같은데.”

“뭐 그렇게 생각하는 사람이 많은데 굉장히 공부도 많이 하고 경험도 많아서 엄청 잘해. 소스를 섞거나 샘플을 사용하는 센스가 무지 좋아.”

“오호. 갑자기 멋있어 보이네요.”

“원래 음악 잘하면 멋있어 보이지.”

“저번주에 숙제를 해왔는데 제대로 했나 모르겠어요. 조금 헷갈리기도 하고. 다시 한번만 설명해 주세요.”

“그래. 음정에 관해서 공부했었지?"

"맞아요. 메이저스케일을 이용해서 문제를 풀었었어요.“

"그럼 문제를 한 번 같이 풀어보자.“

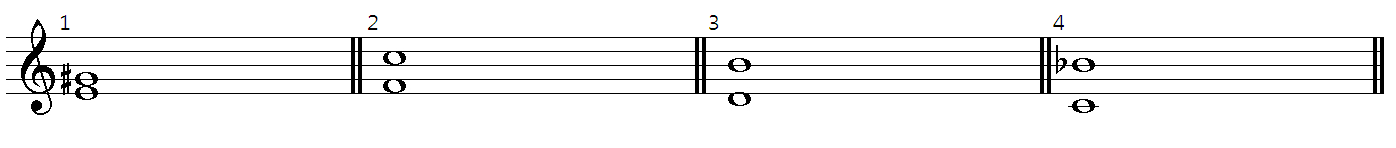
“위의 악보에서 1번 문제를 봐.”

“E와 G#이군요.”

“그래. 우선 몇도인지 숫자부터 세보도록 해.”

“미, 파, 솔#이니까 3도가 되지요?”

“그래. 이제 무슨 3도인지를 맞춰야지. E메이저 스케일에서 G#이 3번째 음이 되니까 장3도가 되는거야.”

“만약 G#이 아니고 G가 되면 어떻게 되나요?”

“G#이 반음이 내려가면 전체적인 간격은 반음만큼 좁아지기 때문에 지난주에 배운 표에서 보듯이 단3도가 되는거야.”

“2번문제는 제가 풀어볼게요. F G A B C 니까 일단 숫자는 5도가 되구요. F메이저 스케일에서 C는 5번째 음이 되니까 장5도인가요?”

“장5도라는 것은 없고 완전5도가 돼.”

“아, 맞다. 2367도 일 때만 장(단)이 붙었지요.”

“그럼 푸는 김에 3번도 풀어보자.”

“D, E, F, G, A, B이니까 숫자는 6도가 되고, D메이저스케일에서 여섯 번째 노트가 B이니까 장6도입니다.”

“나머지 4번도 풀어보자.”

“도, 레, 미, 파, 솔, 라, 시b이니까 7도가 되고, C메이저스케일에서 일곱 번째 노트는 B이니까 B라면 장7도가 됩니다. 그런데 B에서 b(플랫)이 붙어서 전체간격이 반음 줄어들었기 때문에 단7도가 됩니다.”

“좋아, 이제 음정의 나머지 부분을 공부해보자. 숙제를 하면서 상행과 하행의 음정을 같이 구하는 문제가 있었지?”

“예, 그 문제를 풀면서 뭔가 공식이 있는 것 같은 느낌이 들더라구요.”

“맞아. 그걸 ‘음정의 자리바꿈’ 혹은 ‘전회음정’이라고 하지. 아래 그림은 원래 음정을 자리바꿈 한거야.”

“1번은 ‘C와 E’ 2번은 ‘E와 C’로 서로 자리바꿈이 된 형태야. 1번의 음정은 어떻게 되지?”

“장3도이군요.”

“맞아. 그럼 2번의 음정은?”

“E메이저스케일에서 6번째 나오는 음이 C#이니까 E와 C는 단6도 인가요?”

“잘했어. 그럼 3번과 4번을 보자. 이것도 자리바꿈이 된 형태야. 각각 음정을 계산해 봐.”

“3번은 완전5도이고 4번은 완전4도에요.”

“자. 그럼 음정이 자리바꿈 할 때 어떤 공식을 따르는지 한번 정리해 보자.”

장음정 ←→ 단음정
완전음정 ←→ 완전음정
증음정 ←→ 감음정

자리바꾸기 전 도수 + 자리바꾼 후 도수 = 9

“자 그럼 내가 문제를 하나 내볼게. B하고 C의 음정은?”

“그건 너무 쉽잖아요. 반음 관계이니까 단2도입니다.”

“좋아, 그럼 그걸 자리바꿈 하면?”

“단은 장이 되고 숫자의 합이 9가 되어야 하니까 장7도인가요?”

“맞았어. 자리바꿈 공식을 알면 6도나 7도도 금방 찾을 수 있을거야.”

“오호. 그나저나 이런 신기한 공식이 있었군요.”

“그래. 적어놓고 보면 별거 아니지. 금방 외워질거야.”

“음악이론에도 외워야 할 것이 참 많네요.”

“사실 외우거나 이론자체를 배우는 것은 이론치고 어렵지 않은데 이것을 몸에 익히는 것이 상당히 오래걸리지.”

“그렇군요. 그래도 지금까지 배운것들 중에는 그런 것이 없겠죠?”

“그럴 리가 있나! 뭐 악기를 가르쳐주는 입장이 아니고 진도를 나가야 하기 때문에 지나가긴 했지만 메이저 스케일을 악기로 연주하고 소리로 듣고 구분할 수 있어야 돼. 뿐만 아니라 각 음정을 소리로 듣고 구분할 수 있어야 돼.”

“소리만 듣고 ‘완전5도’, ‘장7도’ 이런 것을 맞출 수 있어야 하나요?”

“물론. 그게 바로 청음이야. 그래서 많은 사람들이 악기연주를 권하는 거야. 악기를 많이 연주하다보면 자연스럽게 청음능력이 생기거든. 화성학을 몸에 익히기 위해서는 악기연주만한 것이 없지. 앞으로 배울 화음과 텐션 등도 마찬가지야.”

“그렇군요. 드럼패드말고 피아노를 먼저 사야겠어요.”

“그래. 한참 배우는 입장이니 화성학으로 배운 것을 항상 피아노나 기타로 연주해보는 버릇을 들이도록 해.”

“명심하겠습니다!”

“자 이제 좀 더 간격이 넓은 음정에 대해 공부해보자. 옥타브라는 말 혹시 들어봤어?”

“‘도, 레, 미, 파, 솔, 라, 시, 도’에서 낮은 도와 높은 도가 옥타브 관계 아닌가요?”

“맞았어. 위와 같은 경우는 한옥타브 차이가 난다고 말하지. 메이저 스케일에서 8번째 오는 음은 처음 시작하는 음이 되기 때문에 octa(8)라는 단어를 쓰는거야. 요즘에 코어가 8개달린 cpu를 옥타코어라고도 하잖아.”

“제 컴퓨터 맞춘지 얼마 안되서 옥타코어에요!”

“(못 들은 척)음정이 옥타브 이상 벌어지는 걸 ‘겹음정’이라고 하고 그동안 우리가 배웠던 것처럼 옥타브 이내의 음정을 ‘홑음정’이라고 해. 겹음정은 기본적으로 홑음정과 같다고 생각하면 이해가 쉬울거야. 완전, 장, 단, 증, 감, 겹증, 겹감이 붙는 것은 동일하고, 그 대신 숫자만 좀 커지는 거지. 그리고 내껀 듀얼코어야.”

“앗, 말이 너무 빨라서 잘 못들었어요. 한번만 다시 설명해 주세요.”

“듀얼코어라고! 그래도 울프데일이야.”

“CPU말고 화성학이요.”

“아, 그렇지. 가수 세븐 좋아해?”

“세븐이요? 저는 비가 더 낫던데.”

“겹음정 할 때는 무조건 세븐이야.”

“무슨 말씀이신지.”

“자, 일단 악보를 보자.”

“1번은 도수를 세보면 8도 이고 스케일상에 나오는 음이니까 완전8도야. 2번을 한번 해보겠어?”

“‘도, 레, 미, 파, 솔, 라, 시, 도, 레‘니까 9도인건 알겠는데 그 앞에는 뭐가 붙어야 될지 모르겠네요.”

“겹음정도 기본적으로 홑음정과 같으니까 도와 레의 음정을 따져보면 돼. 도와 레는 몇도지?”

“도와 레는 장2도이지요. 아하, 그럼 2번은 장9도 인가요?”

“맞아. 그럼 겹음정 문제를 더 쉽게 푸는 방법을 가르쳐주지.”

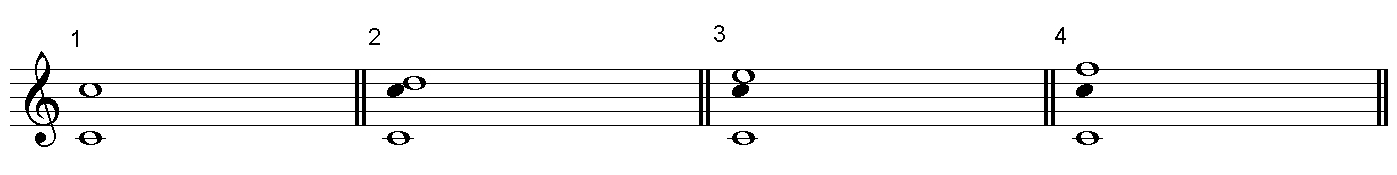
“겹음정 문제를 발견하면 그냥 무조건 한옥타브 올려서 문제를 풀면돼. 아래에 있는 C를 위로 올리면 검은색 노트와 같이 나타낼 수 있지. 여기에서 다시 홑음정이라고 생각하고 문제를 푸는 거야. 3번을 해봐.”

“도,레,미 니까 3도이고 스케일에 있는 음 그대로 이니까 장3도네요.”

“그래. 그럼 이제 세븐이 나올때야.”

“7을 더하면 되나요?”

“장3도에서 7도를 더하면 장10도가 되지. 그게 3번 문제의 정답이야. 4번도 한번 풀어봐.”

“C와 F이니까 완전4도이고, 7을 더하면 완전 11도가 되네요.”

“잘했어. 그러면 이제 겹음정 문제도 쉽게 풀 수 있겠지?”

“풀....수 있겠지요?”

“오늘 수업은 여기까지 하자. 음정은 문제를 많이 풀어보고 소리를 많이 들어서 정확히 구분하는 게 중요해. 문제를 100문제 풀면 100문제 다 맞힐 수 있을 정도로 확실하게 공부해 두도록 해. 소리를 듣는 것은 오래 걸리겠지만 꾸준히 하다보면 많이 나아질거야. 처음에 안된다고 금방 포기하지 말고 꾸준히 할 수 있도록 해. 그리고 혹시 음정 계산이 빨리 안된다 싶으면 메이저 스케일부터 다시 확실하게 외우는게 좋아. 혹시 질문이 있나?”

“음정 문제 중에서 위아래 임시표가 복잡하게 붙어있는 문제는 어떻게 풀어야 하나요?”

“그건 문제를 자주 풀다보면 자연스럽게 알게 될거야. 다만 팁을 몇 개 가르쳐 줄게.”

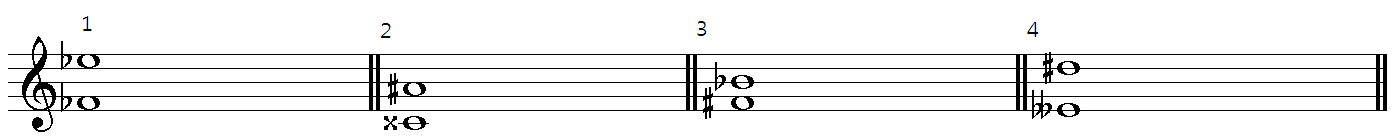
“위의 악보에서 첫 번째 문제를 봐. Fb메이저 스케일이라는 건 없기 때문에 메이저스케일로 따지기가 좀 곤란하지.”

“Fb은 E하고 같으니까 E메이저스케일을 이용하면 안되나요?”

“음정문제를 풀 때 도수는 바뀌지 않아. 그래서 1번 문제에서 나오는 숫자 7도는 바뀌면 안돼. E라고 해버리면 7도가 8도가 되어 버리기 때문에 그렇게하면 안되고 이런 문제에서는 임시표를 지워버리면 돼.”

“임시표를 지운다구요?”

“음정은 영어로 interval, 즉 간격이기 때문에 위아래로 같은 임시표가 붙어있을 때는 없다고 생각하면 편하지. 임시표가 없다고 생각하면 F메이저스케일을 이용해서 장7라는 것을 쉽게 구할 수 있어.”

“아하, 그렇군요.”

“위 아래 다른 임시표가 붙어있는 경우에도 아예 임시표가 없다고 생각하면 편하지. 2번도 마찬가지야. 더블샵이 붙어있어서 복잡해 보이지만 일단 임시표가 없다고 생각하면 장6도가 되지. 거기에서 위아래 같은 임시표는 상쇄되기 때문에 아래쪽에만 샵이 하나가 남게 돼. 아래쪽에 샵이 붙으면 전체 간격이 좁아지니까 단6도가 되는거야. 3번도 한번 풀어봐.”

“임시표가 없다고 생각하면 F B니까 증4도가 되는군요. 아래쪽에 샵이 붙고 위쪽에 플랫이 붙으니 간격이 반음+반음만큼 줄어들게 됩니다. 그럼 완전4도가 됐다가 다시 감4도가 되네요.”

“잘하고 있군. 4번도 해봐.”

“4번도 임시표가 없다고 생각하면 단7도가 되네요. 아래쪽에 더블플랫이 붙고 위쪽에 샵이 한번 붙으니 반음이 세 번만큼 넓어집니다. 그러면 장7도가 되고 다시 증7도가 됐다가 결국 겹증7도가 됩니다.”

“너무 잘하니까 가르치는 재미가 없군.”

“아니에요. 잘하긴요. 근데 잘하는 쪽이 가르치는 게 재밌는거 아닌가요?”

“내가 할 말이 줄어들잖아. 안그래도 수다 떨 친구도 없는데.”

“요새 많이 심심하신 모양이군요.”

“뭐 아니라고는 못하겠군. 그럼 오늘 수업은 여기까지 하자. 숙제는 꼭 해오도록 해.”

HOME WORK

1. 다음 음정의 전회음정을 구하세요.

① m3

② P5

③ M6

④ M3

⑤ A4

⑥ P8

⑦ m2

⑧ P4

⑨ M2

⑩ M7

2. 다음 음정을 구하세요.

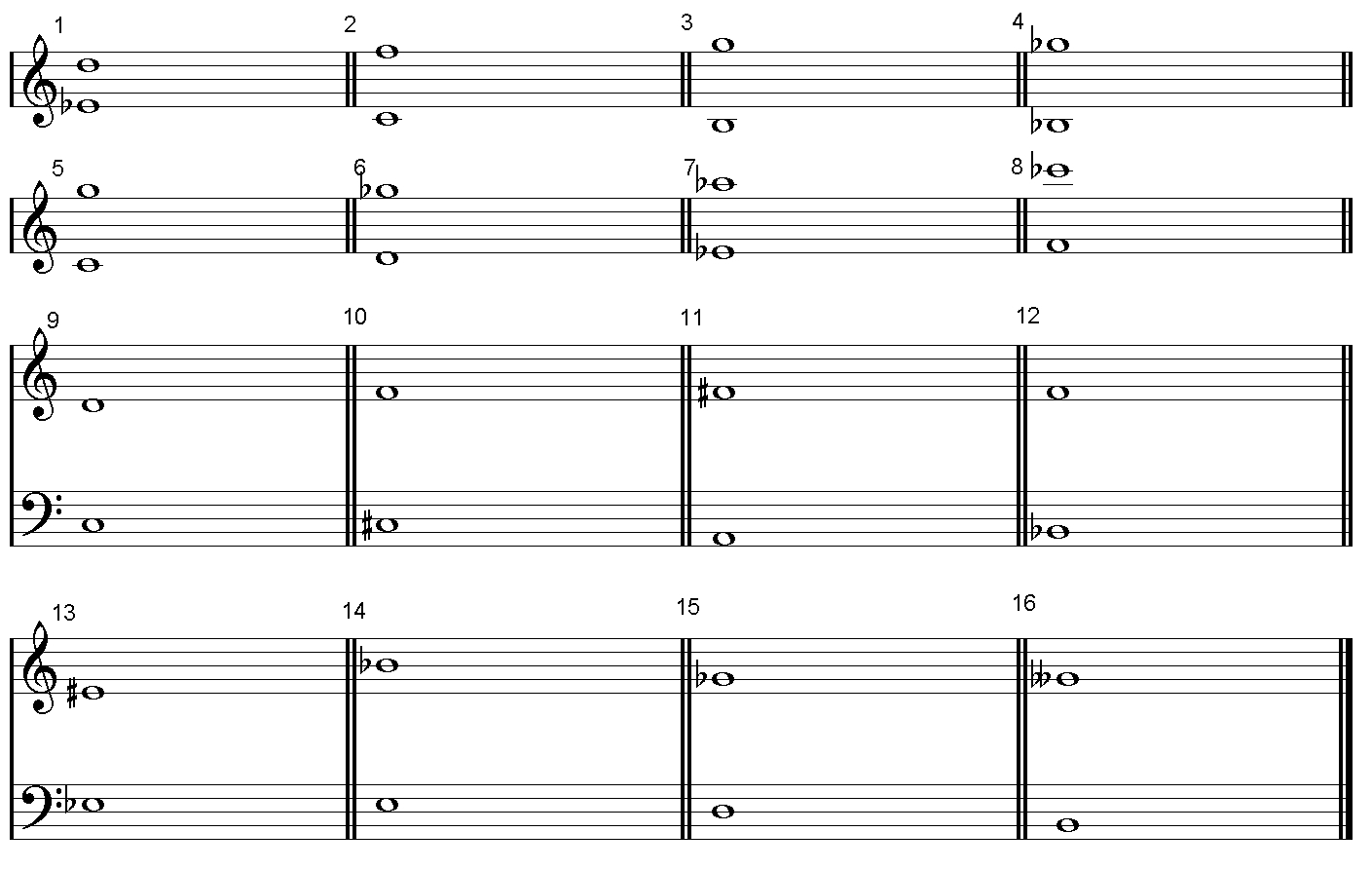
3. 다음 주어진 음에 장3도 위의 음을 구하세요.

4. 다음 주어진 음에 완전5도 위의 음을 구하세요.

5. 다음 주어진 음에 장9도 위의 음을 구하세요.

6. 다음 주어진 음에 완전11도 위의 음을 구하세요.

7. 다음 주어진 음에 단13도 위의 음을 구하세요.

8. 다음 주어진 음에 증11도 위의 음을 구하세요.

정답링크 : https://bonik.me/569

#음정 #화성학 #Interval